The direct simulation Monte Carlo (DSMC) method, developed by Graeme A. Bird, is a well-established stochastic approach to modeling the Boltzmann transport equation (BTE). DSMC simulates particle collisions and motions in a decoupled manner and all flow information is derived from the ensemble average of individual particle data. Each computational DSMC particle represents a large number of physical particles having the same properties to reduce computational cost. The DSMC method accurately and efficiently models molecular transport and thermochemical nonequilibrium, especially for low-density (rarefied flows). DSMC converges to the solution of BTE when the number of DSMC particles is very large to reduce statistical fluctuations using massively parallel computing facilities. Therefore, the DSMC method is applicable to a wide Knudsen number spectrum of values including the micro-electro-mechanicals systems to space applications such as jet expansions, plumes of electric propulsion devices, re-entry, etc.
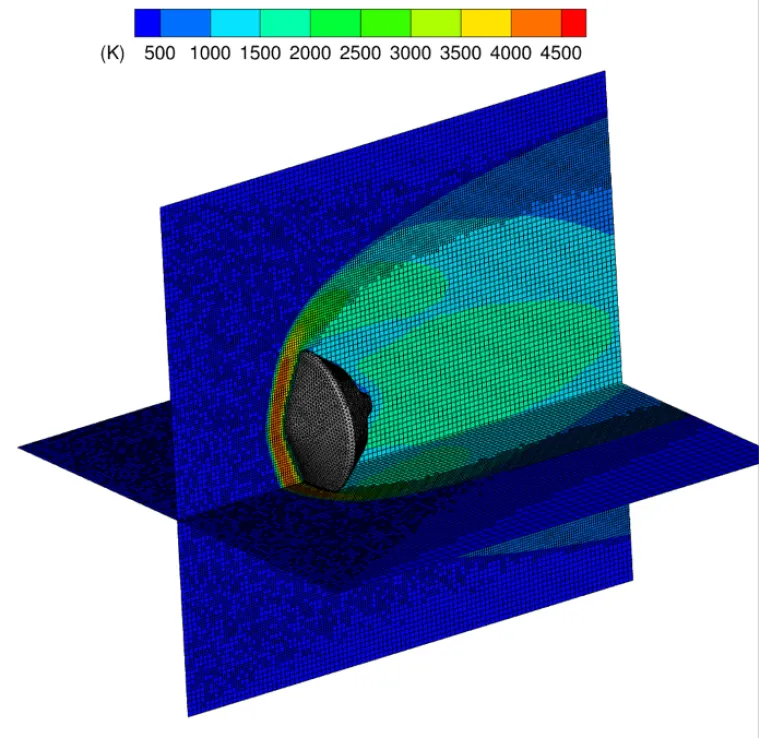
Spatial distribution of the translational temperatures for the Mars Science Laboratory (MSL) for the mixture of CO2 and N2 at Mach 5 using the SPARTA DSMC software.
CHANL actively uses the DSMC method for rarefied flow applications. Due to the sudden expansion of flow in wakes, the continuum assumption breaks down and the solution of BTE provides accurate results. As shown in the figure, the on-the-fly grid adaptation of SPARTA captures large gradients in the temperature field of a CO2 and N2 mixture. The presence of multiple length scales and recirculation also results in distinct temporal variations which, in turn, affect the dynamic stability of vehicles, especially during re-entries. To investigate the time characteristics of vortex shedding, different flow conditions were studied, as shown below.
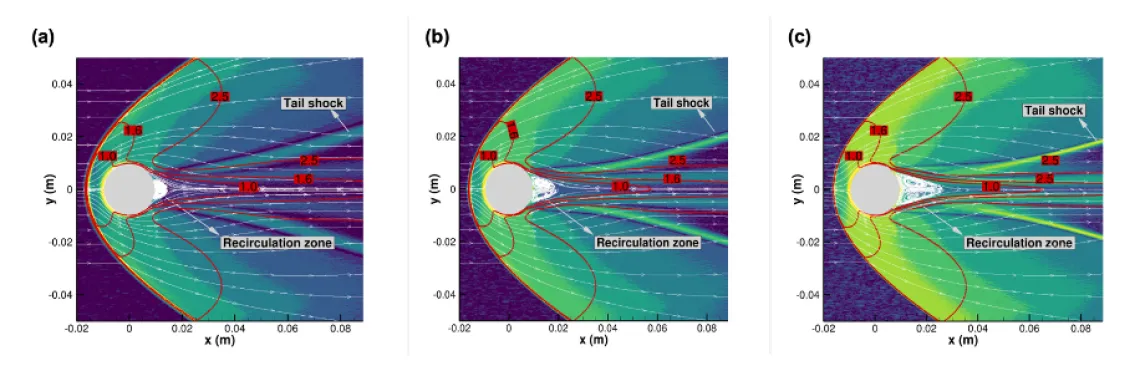
Spatial distribution of the density magnitude gradient along with the Mach number lines and streamlines in the vicinity of the recirculation region for Mach number of 7 at different freestream pressure values (a) 25 Pa, (b) 50 Pa, and (c) 100 Pa, using DSMC.
